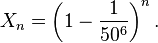Els
nombres normals són aquells irracionals que tenen una expressió decimal
infinita en la que totes les xifres apareixen amb la mateixa freqüència. Com
que els nombres es poden escriure en diferents bases (base 2 o base 10, per
exemple), direm que un nombre és absolutament
normal quan ho és en totes les bases. En la definició hem d’incloure
no solament les xifres sinó els grups de xifres. Per exemple si un nombre és
normal en base 10 hem d’esperar que totes les xifres de la 0 a la 9 apareguin
(quan se’n examinen moltes) amb una freqüència de 1/10 i tots els grups de dos
xifres de 00 a 99 amb una freqüència de 1/100. Etc. Com exemple de nombre decimal normal en base
10: 0,1234567891011121314151617181920…
Es
produeix un fenomen curiós del qual ja ens va parlar Kac en el 1959: “Sovint és
més fàcil demostrar que un gran nombre d’objectes tenen una determinada
propietat que exhibir-ne un de concret que la tingui.”
Émile
Borel va demostrar el 1909 que quasi tots els reals són (absolutament) normals.
Tècnicament el que va demostrar és que el conjunt de reals no normals té mesura de Lebesgue zero. Això voldria dir que
si els poséssim tots junts la longitud del segment que ocuparien seria zero.
Malgrat això el conjunt dels nombres no normals no és numerable. Per exemple,
el conjunt dels nombres entre 0 i 1 que no tenen la xifra 5 en la seva
expressió decimal no és numerable i tots són no normals.
De
fet, però, (recordem Kac) és molt difícil demostrar que un nombre és
absolutament normal. Se sospita que π (pi) ho és i s’ha vist que les seves
xifres, fins on s’han calculat, segueixen aquesta regla de freqüències, com si
haguessin estat generades aleatòriament. Les constants de Chaitin, de les quals
ara no en parlarem, són normals però és tracta d’uns nombres, encara que ben
definits, que no són computables: cap programa d’ordinador pot anar generant
les seves xifres. El 2002 Becher va construir un nombre normal computable, però
la construcció no donava les seves xifres.
Cenyim-nos
ara a la base dos, on les úniques xifres són zeros i uns. Imaginem una successió qualsevol de zeros i
uns que tingui mil termes. Hi ha 2 (exponent 1000) successions així i, per
tant, si el nombre és normal la freqüència amb la que apareixerà aquesta
successió serà 1/ 2(exponent 1000), un nombre molt petit, però com que estem
parlant d’infinites xifres, aquesta seqüència ha d’acabar apareixent amb
probabilitat 1. I ara ve la sorpresa. Estem a la època digital i, per tant, no
ens és estrany que qualsevol cosa de la nostra vida diària es pot digitalitzar.
Per exemple, Hamlet. Per tant, arribem a la conclusió que si π és normal, en la seva expressió decimal en base binària tenim
codificat Hamlet (amb probabilitat 1). I no solament en versió anglesa, sinó en
la catalana, la xina, etc. I tots els teoremes de les matemàtiques, que no són
altra cosa que una successió de símbols i que també es poden codificar, estan,
amb probabilitat 1 en la successió de π, (o de qualsevol nombre normal i ja
sabem que quasi tots el nombres reals són normals). Però no solament els
teoremes coneguts sinó els que ens queden per descobrir, les obres de
literatura que ens queden per escriure, els quadres que s’han pintat o ens
queden per pintar, etc.
No
és sorprenent? Si π és normal, la probabilitat de que tot el saber i la
cultura humana estiguin codificats en la seva successió de xifres és 1.
El
que acabem de dir està relacionat amb el teorema del mico infinit. Un mico teclejant a l’atzar en una màquina d’escriure
acabarà escrivint Hamlet. El mico no és més que una metàfora. Es tracta de
veure si fent que la màquina teclegi totalment a l’atzar aquesta acabarà
escrivint alguna cosa important. Examinem-ho. Imaginem que la màquina té 50
tecles i mirem la probabilitat de que teclegi una determinada paraula de 6
lletres com “nombre”.
Amb
suficient temps un mico, escrivint a l’atzar, acabarà escrivint Hamlet
La
probabilitat de que les primeres 6 lletres teclejades sigui “nombre” és:
(1/50) × (1/50) × (1/50)
× (1/50) × (1/50) × (1/50) = (1/50)6 =
1/15 625 000 000,
un
nombre molt petit, però no és zero.
Per tant, la probabilitat de no teclejar nombre
en un determinat grup de 6 lletres es 1 − (1/50)6. Com que
els grups es teclegen independentment, la probabilitat Xn de
no teclejar nombre en qualsevol dels
primers n grups of 6 lletres és:
Quan n creix, Xn esdevé més i més
petit. Per a n igual a 1.000.000, Xn és aproximadament
0.9999, però per a n =
10.000.000.000 Xn és aproximadament 0.53 i per a n
= 100.000.000.000 és 0,0017. Quan n s’aproxima infinit, la probabilitat Xn s’acosta a zero i, per
tant, és pràcticament segur que la màquina d’escriure teclejarà “nombre”.
El que hem dit val per qualsevol text, per llarg que sigui.
Ara bé, com que el text de Hamlet té unes 130.000 lletres, ignorant les
puntuacions, espais i majúscules hem de teclejar les 26 lletres de l’alfabet
anglès. La probabilitat d’ encertar-lo a la primera és de una en 3.4 × 10183,946
La mitjana de lletres que hem d’escriure
abans de que aparegui el text amb puntuació és 4.4 × 10360,783
Per dir-ho d’una altra manera, per a
tenir una probabilitat de una en un bilió d’èxit, hauríem d’emplear tants micos
com àtoms té l’univers en 10360,641
universos com el nostre. Al final resulta que la cultura humana no és tan fruit
de l’atzar com semblava.